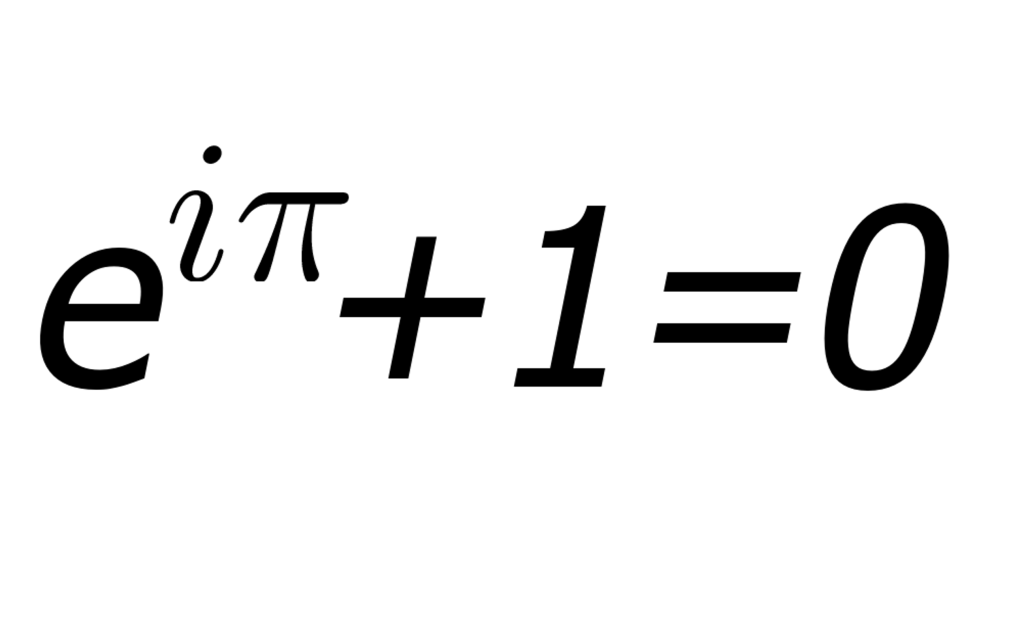Too many eggs in one basket

My daughter, Maddie, will be turning 22 on Sunday, April 10. She is the oldest of our four children. When she was just 9 years old we bought her a dog. Ruby, the dog (not my daughter … remember her name is Maddie), is blind in one eye (she thinks she’s look at the camera) and generally can’t hear, but she has three younger brothers (that’s true for both Maddie and Ruby) to keep her acting like a puppy (Ruby – not Maddie). My oldest son Christian has a dog, Jake. My two youngest sons, Sean and Finn, have twin dogs, Rider and Comet. Needless to say we are a dog family. So what happens when our children grow up and out of the house? How can we take four dogs and divide them among six people?

Most 3rd graders should be able to attempt this problem, but not solve it “correctly”. What about 4th graders? 5th graders? … High school?

Of course if we enact our skills of extracting critical information from the situation (does it matter what ailments Ruby has or how old my daughter was when she got her?), and then apply the algorithm of either “repeated” subtraction or the notion of fair-share, we realize each one of my family members (myself included) would be able to cuddle up with just 2/3 of a dog once properties of division are satisfied and we all agree fractions are numbers too. The math makes sense, but I really hope you see a problem with a fractional solution in this unrealistic situation. The real (non-mathematical) answer is that my wife and I keep all four dogs.

In 2001, the National Research Council published Adding it Up: Helping Children Learn Mathematics as a guide for educators to rethink how mathematics should be taught in grades pre-K through 8. The core of the text suggests there are five strands that are necessary for learning mathematical concepts.

Students spend a lot of time practicing procedural fluency, but under the auspices of standardized testing and time constraints we convince ourselves the other strands will either come naturally as students mature … or just aren’t as important as being able to do the math in order to get the right answer.

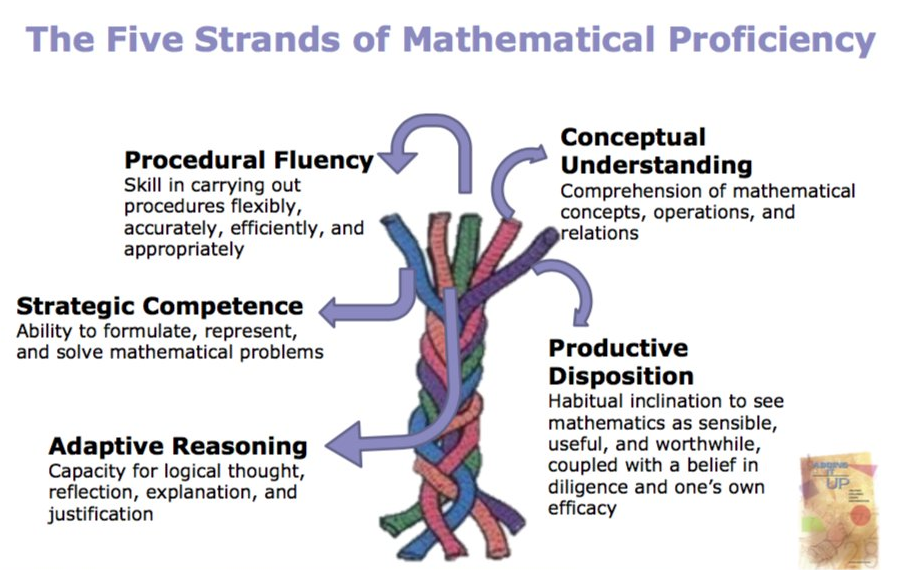
Graham Fletcher presented some of his learning progressions at the Montgomery County Intermediate Unit recently. This image of Graham shows a simplified form of the five strands where Application serves as a big bucket category for strategic competence, adaptive reasoning and productive disposition.

Graham Fletcher presenting at the MCIU on March 29, 2022.

Building authentic context around problems, and engaging students in modeling and conceptual understanding offers greater opportunity for students to participate in their learning. The introduction of design thinking, project based learning and interdisciplinary teaching and learning may be a bit of a stretch right now. Consider the dynamics of your classroom, and the balance of rational thinking versus algorithmic thinking that you expect from your students on a daily basis.

Can you infuse experiences that allow students to develop critical thinking (effect size = 0.49) and exercise creativity (effect size = 0.58)? Have you tried 3-Act math activities? They are built into the enVision program already, and if you’re looking for more check out Graham Fletcher, Andrew Stadel, Robert Kaplinsky (Open Middle is another activity worth exploring) and of course Dan Meyer. If 3-Act math is old news, let’s now consider design challenges and project based or problem based experiences. As unique as each of our individual students can be, the experiences we design for them can be just as unique. Let’s start scrambling the content, strategies, and experiences into authentic and holistic learning moments to get out of the eggs-in-one-basket approach to education.

Postscript: if you’re looking for resources on design thinking and project based learning for your classroom, I’ll be posting additional content to help (sorry to leave you hanging at the moment) … but we can always use your help in creating new experiences. If you’re interested in helping, please reach out.

“3 and a bit”

How is pizza related to pi? (image source: Veritasium youtube channel)

We all know about pi and its common numerical equivalent for practical purposes (3.14). But where did pi come from, and why? The development of pi over the centuries is an example of mathematical innovation. As you know, today is Pi Day. If you’re interested in links to help students engage in pi for Pi Day, skip to the bottom. If you want to know a bit more about pi … keep reading.

First, pi is the ratio of a circle’s perimeter to its diameter.

The short history is pi was first approximated by the area of polygons with n=6 sides (a hexagon) that is inscribed (inside a unit circle with diameter = 1) and circumscribed (around the same circle). Pi was approximated to be between 3 and 4. Over a long stretch of time the polygon was bisected and bisected and bisected … and you get the point. The last time this method was used to approximate pi is in 1630 using a polygon with n=10⁴⁰. At this time, pi had 38 digits to the right of the decimal, but it took over 25 years to make this approximation.

That’s a long time to simply calculate a very precise numerical representation of pi. Here is where the innovation happens. In 1666 Sir Isaac Newton, while recovering from Bubonic plague (what discoveries may come from the conditions Covid-19 placed on society?) decides there has to be a better way. Through widespread understanding of Pascal’s triangle and the development of the binomial theorem, Newton “breaks” the rules of algebra, and applies calculus to the geometric theories of circles, and discovers the irrational nature of pi allowing anyone with a computer to calculate pi to whatever level of precision they desire. I’m sure everyone can find pi on a calculator.

This isn’t about how many digits of pi we can calculate, but rather to recognize that something as mundane as pi has a rich history of innovation that allows anyone to use it in its most simplistic form (3.14) in the discovery, creation and invention of both simple and complex ideas. Newton provides an example of how the following three aspects of mathematical innovation come together for a discovery that is now used by every student across the globe.

Arte Scienza – development of balance between science and art, logic and imagination. [Pascal’s triangle and the binomial theorem]

Conneccione – everything is connected to everything else. [pi is an amalgamation of algebra, geometry and calculus]

Curiosita – the curiosity to find the connections. [Newton was curious about how to calculate pi without the arduous task of bisecting polygons]

This line of thinking allows mathematical and scientific innovation to propagate into other disciplines. Here is a brief timeline of pi and it’s uses in other innovations.

Archimedes uses the geometry of a circle to introduce the concept of pi …

Keplar’s laws of planetary motion …

Galileo’s pendulum …

Euler’s use of algebra, trigonometry and geometry to develop Euler’s constant and what some consider the most beautiful formula in mathematics using 5 important constants:

(more on this in a future post)

Gauss’ normal distribution …

Einstein’s theory of relativity!

To hear more about the history of pi and it’s discovery check out the Veritasium youtube channel.

For resources to connect innovations in mathematics with your students check out MoMath .

If you’re looking for activities for Pi Day, What We Do All Day offers some great projects, and Jo Boaler just updated her youcubed website with this Finding Pi activity.